
| Source file: | edge.{c, cpp, java, pas} |
| Input file: | edge.in |
| Output file: | edge.out |
IONU Satellite Imaging, Inc. records and stores very large images using run length encoding. You are to write a program that reads a compressed image, finds the edges in the image, as described below, and outputs another compressed image of the detected edges.
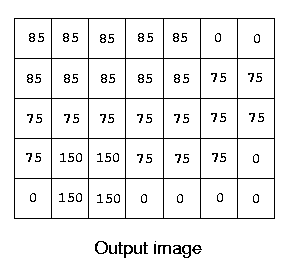
A simple edge detection algorithm sets an output pixel's value to be the maximum absolute value of the differences between it and all its surrounding pixels in the input image. Consider the input image below:


Images contain 2 to 1,000,000,000 (109) pixels. All images are encoded using run length encoding (RLE). This is a sequence of pairs, containing pixel value (0-255) and run length (1-109). Input images have at most 1,000 of these pairs. Successive pairs have different pixel values. All lines in an image contain the same number of pixels.
Input consists of information for one or more images. Each image starts with the width, in pixels, of each image line. This is followed by the RLE pairs, one pair per line. A line with 0 0 indicates the end of the data for that image. An image width of 0 indicates there are no more images to process. The first image in the example input encodes the 5x7 input image above.
Output is a series of edge-detected images, in the same format as the input images, except that there may be more than 1,000 RLE pairs.
Important Note: A brute force solution that attempts to compute an output value for every individual pixel will likely fail due to space or time constraints.
Example input:
7 15 4 100 15 25 2 175 2 25 5 175 2 25 5 0 0 10 35 500000000 200 500000000 0 0 3 255 1 10 1 255 2 10 1 255 2 10 1 255 1 0 0 0
Example output:
7 85 5 0 2 85 5 75 10 150 2 75 3 0 2 150 2 0 4 0 0 10 0 499999990 165 20 0 499999990 0 0 3 245 9 0 0 0
Last modified Fri Oct 27 15:13:04 2000