Problem D: Su-domino-ku

As if there were not already enough sudoku-like puzzles, the July 2009 issue of Games Magazine describes the following variant that combines facets of both sudoku and dominos. The puzzle is a form of a standard sudoku, in which there is a nine-by-nine grid that must be filled in using only digits 1 through 9. In a successful solution:

• Each row must contain each of the digits 1 through 9.
• Each column must contain each of the digits 1 through 9.
• Each of the indicated three-by-three squares must contain each of the digits 1 through 9.

For a su-domino-ku, nine arbitrary cells are initialized with the numbers 1 to 9. This leaves 72 remaining cells. Those must be filled by making use of the following set of 36 domino tiles. The tile set includes one domino for each possible pair of unique numbers from 1 to 9 (e.g., 1+2, 1+3, 1+4, 1+5, 1+6, 1+7, 1+8, 1+9, 2+3, 2+4, 2+5, ...). Note well that there are not separate 1+2 and 2+1 tiles in the set; the single such domino can be rotated to provide either orientation. Also, note that dominos may cross the boundary of the three-by-three squares (as does the 2+9 domino in our coming example).

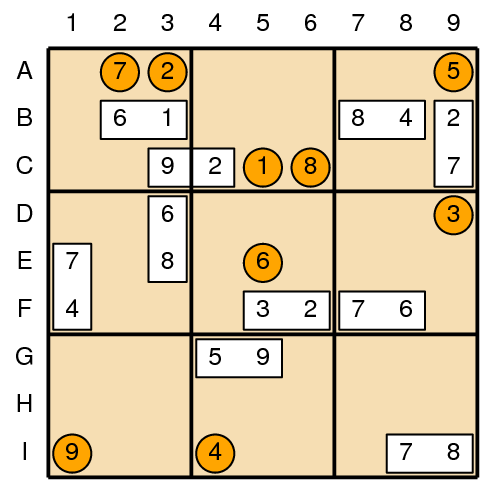
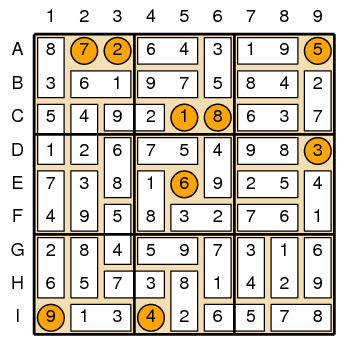
To help you out, we will begin each puzzle by identifying the location of some of the dominos. For example, Figure 1 shows a sample puzzle in its initial state. Figure 2 shows the unique way to complete that puzzle.

Figure 1: Sample puzzle	Figure 2: Solution

Input:  Each puzzle description begins with a line containing an integer N, for 10 ≤ N ≤ 35, representing the number of dominos that are initially placed in the starting configuration. Following that are N lines, each describing a single domino as U LU V LV. Value U is one of the numbers on the domino, and LU is a two-character string representing the location of value U on the board based on the grid system diagrammed in Figure 1. The variables V and LV representing the respective value and location of the other half of the domino. For example, our first sample input beings with a domino described as 6 B2 1 B3. This corresponds to the domino with values 6+1 being placed on the board such that value 6 is in row B, column 2 and value 1 in row B, column 3. The two locations for a given domino will always be neighboring.

After the specification of the N dominos will be a final line that describes the initial locations of the isolated numbers, ordered from 1 to 9, using the same row-column conventions for describing locations on the board. All initial numbers and dominos will be at unique locations.

Output:  For each puzzle, output an initial line identifying the puzzle number, as shown below. Following that, output the 9x9 sudoku board that can be formed with the set of dominos. There will be a unique solution for each puzzle.