Problem A: Pythagoras's Revenge

The famous Pythagorean theorem states that a right triangle, having side lengths A and B and hypotenuse length C, satisfies the formula

A² + B² = C²

It is also well known that there exist some right triangles in which all three side lengths are integral, such as the classic:

Further examples, both having A=12, are the following:

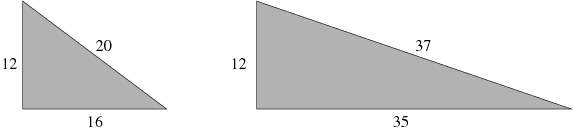
The question of the day is, given a fixed integer value for A, how many distinct integers B > A exist such that the hypotenuse length C is integral?

Input:  Each line contains a single integer A, such that 2 ≤ A < 1048576 = 2²⁰. The end of the input is designated by a line containing the value 0.

Output:  For each value of A, output the number of integers B > A such that a right triangle having side lengths A and B has a hypotenuse with integral length.

A Hint and a Warning: Our hint is that you need not consider any value for B that is greater than (A²-1)/2, because for any such right triangle, hypotenuse C satisfies B < C < B + 1, and thus cannot have integral length.

Our warning is that for values of A ≈ 2²⁰, there could be solutions with B ≈ 2³⁹, and thus values of C² > B² ≈ 2⁷⁸.

You can guarantee yourself 64-bit integer calculations by using the type long long in C++ or long in Java. But neither of those types will allow you to accurately calculate the value of C² for such an extreme case. (Which is, after all, what makes this Pythagoras's revenge!)