Problem G: Cash Cow

Years before Candy Crush became the wildly popular game that may lead developer Saga to a multi-billion dollar IPO, there was an online game named Cash Cow, which remains part of the Webkinz platform.

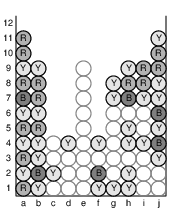
This single-player game has a board with 12 rows and 10 columns, as shown in Figure 1. We label the rows 1 through 12, starting at the bottom, and the columns a through j, starting at the left. Each grid location can either have a colored circle or be empty. (We use uppercase characters to denote distinct colors, for example with B=blue, R=red, and Y=yellow.) On each turn, the player clicks on a circle. The computer determines the largest "cluster" to which that circle belongs, where a cluster is defined to include the initial circle, any of its immediate horizontal and vertical neighbors with matching color, those circles' neighbors with matching colors, and so forth. For example, if a user were to click on the blue circle at cell (h10) in Figure 1, its cluster consists of those cells shown with empty circles in Figure 2.

Figure 1	Figure 2	Figure 3
Processing a click on cell h10.

The player's turn is processed as follows. If the indicated grid cell belongs to a cluster of only one or two circles (or if there is no circle at that cell), the turn is wasted. Otherwise, with a cluster of 3 or more circles, all circles in the cluster are removed from the board. Remaining circles are then compacted as follows:

1. Circles fall vertically, to fill in any holes in their column.
2. If one or more columns have become empty, all remaining columns slide leftward (with each nonempty column remaining intact), such that they are packed against the left edge of the board.

For example, Figure 3 shows the board after the cluster of Figure 2 was removed after the click on (h10).

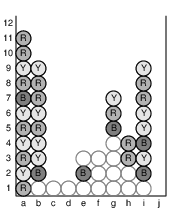
As another example, Figure 4 below, portrays the processing of a subsequent click on cell (j1). During that turn, column (e) becomes empty, and the resulting columns (f) through (j) slide to become columns (e) through (i), respectively. Figure 5 provides one further example in which several columns are compacted.

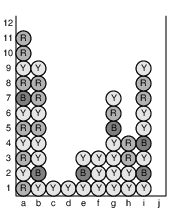Figure 4: Processing a click on cell j1.

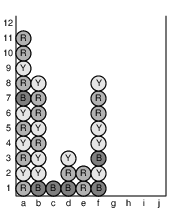Figure 5: Processing a click on cell g2.

Input: The input will consist of multiple games, each played with a new board. For each game, the input begins with a number T that denotes the number of turns that the player will be making, with 1 ≤ T ≤ 20. Following that will be an initial board configuration, which always has 12 rows and 10 columns per row, with uppercase letters used to denote distinct colors. There will never be empty cells within the initial board. Following the presentation of the initial board will be T additional lines of input, each designating a cell of the grid; we rely on the coordinate system illustrated in the above figures, with a lowercase letter, from a to j, denoting a column and a number from 1 to 12 that denotes a row. We note that if a player clicks on a grid cell that does not currently have any circle, that turn is simply wasted.

The end of the entire input will be designated by a line with the number 0.

Output: For each game, output a single line designating the the number of circles that remain on the board after all of the player's turns are processed.

3
RYBBRBYYRY
RRRBBBBBRR
YRRBRBBBBR
RYYBRYYRYY
BRBBRBRBRY
YYBYRBBRRB
RYBBBBRYYY
YBRBRBRYRB
RYBBBBBBBY
YBBRRRRRBB
RBBRRBRYRR
BBBRRYYYRR
h 10
j 1
g 2
3
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYBYYBBBBB
YYBYYBBBBB
c 2
c 12
g 1
2
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYYYYBBBBB
YYBYYBBBBB
YYBYYBBBBB
g 1
c 12
0

33
62
2