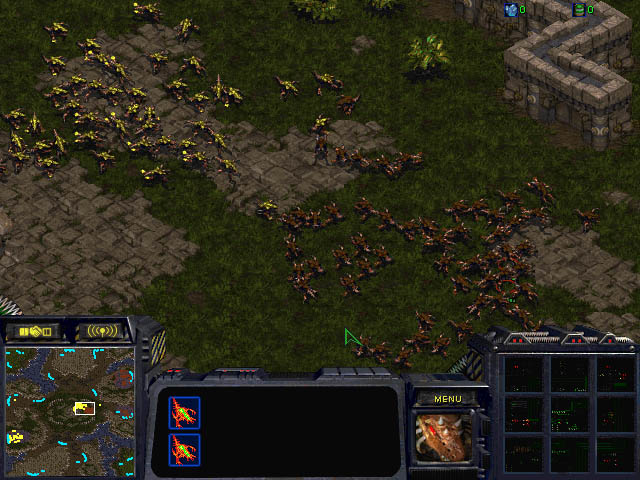
 A typical strategy in the game Starcraft is to mass up large amounts
of low-tier units such as Zerglings, then throw them at your opponent
and laugh maniacally as they overwhelm any opposition. However, when
both players opt for the same strategy, the result can often
become...quick, brutal and messy. Sadly, the game only allows for up
to 400 Zerglings per player. In this problem, however, you will simulate
games that could have more than 400 Zerglings.
A typical strategy in the game Starcraft is to mass up large amounts
of low-tier units such as Zerglings, then throw them at your opponent
and laugh maniacally as they overwhelm any opposition. However, when
both players opt for the same strategy, the result can often
become...quick, brutal and messy. Sadly, the game only allows for up
to 400 Zerglings per player. In this problem, however, you will simulate
games that could have more than 400 Zerglings.
The map on which Zerg rushes occur is represented by a NxN grid. Each Zergling occupies a grid square and no two Zerglings ever occupy the same grid square. Each Zergling has a certain number of hit points which starts off as 35. Its attack value is 5 plus the attack upgrade of the player that controls it. When one Zergling attacks another, the damage incurred equals to the attack value of the attacking Zergling minus the armour upgrade of the player that owns the Zergling being attacked. The number of hit points of the Zergling that is attacked is reduced by the amount of the damage.
Due to the inability of both players to manage their huge horde of Zerglings, the Zerglings make their decisions each turn using the following algorithm (Zerglings are not the brightest creatures, as you will see):
Once all Zerglings have made their decisions, all the attacks are conducted simultaneously and all the Zerglings with 0 or fewer hit points are marked as dead and removed from the map. Then all the movements of the Zerglings that didn't attack are conducted simultaneously. If the square to which a Zergling is moving is occupied by another Zergling that is not moving away in this turn, then the Zergling does not move. If two or more Zerglings try to move to the same grid square, then the Zergling in the northernmost row has the right of way and the other Zergling remains stationary. If there are multiple Zerglings in the northernmost row trying to move to the same grid square, then of these, the westernmost Zergling moves and the others remain stationary. Zerglings also have a remarkable regeneration rate. After each turn, all the Zerglings that are still alive and have less than 35 hitpoints will regain one hit point.
2 0 0 0 0 1. .. 0 2 0 0 0 0 1. .2 100 0
1. .. .. ..