Problem D: Knight's Trip
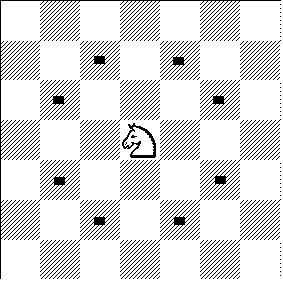 In chess, each move of a knight consists of moving by two squares
horizontally and one square vertically, or by one square horizontally
and two squares vertically. A knight making one move from location (0,0) of an
infinite chess board would end up at one of the following eight locations:
(1,2),
(-1,2),
(1,-2),
(-1,-2),
(2,1),
(-2,1),
(2,-1),
(-2,-1).
In chess, each move of a knight consists of moving by two squares
horizontally and one square vertically, or by one square horizontally
and two squares vertically. A knight making one move from location (0,0) of an
infinite chess board would end up at one of the following eight locations:
(1,2),
(-1,2),
(1,-2),
(-1,-2),
(2,1),
(-2,1),
(2,-1),
(-2,-1).
Starting from location (0,0), what is the minimum number of moves required
for a knight to get to some other arbitrary location (x,y)?
Input Specification
Each line of input contains two integers x and y, each with
absolute value at most one billion. The integers designate a location
(x,y) on the infinite chess board.
The final line contains the word END.
Sample Input
1 2
2 4
END
Output Specification
For each location in the input, output a line containing one integer,
the minimum number of moves required for a knight to move from
(0,0) to (x, y).
Output for Sample Input
1
2
Ondřej Lhoták

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.
 In chess, each move of a knight consists of moving by two squares
horizontally and one square vertically, or by one square horizontally
and two squares vertically. A knight making one move from location (0,0) of an
infinite chess board would end up at one of the following eight locations:
(1,2),
(-1,2),
(1,-2),
(-1,-2),
(2,1),
(-2,1),
(2,-1),
(-2,-1).
In chess, each move of a knight consists of moving by two squares
horizontally and one square vertically, or by one square horizontally
and two squares vertically. A knight making one move from location (0,0) of an
infinite chess board would end up at one of the following eight locations:
(1,2),
(-1,2),
(1,-2),
(-1,-2),
(2,1),
(-2,1),
(2,-1),
(-2,-1).
